
เป็นที่ทราบกันดีมานานแล้วว่า คณิตศาสตร์นั้นเป็นหลักการสากลที่อยู่เบื้องหลังปรากฏการณ์ธรรมชาติต่าง ๆ ซึ่งสามารถนำมาใช้อธิบายได้แม้กระทั่งแบบแผนการเกิดรูปทรงของสิ่งมีชีวิต อย่างเช่นที่ลำดับฟีโบนัชชี (Fibonacci sequence) กำหนดลักษณะการเรียงตัวของตาสัปปะรด เมล็ดทานตะวัน และลูกสน ด้วยสัดส่วนตัวเลขที่เป็นผลรวมของจำนวนในสองลำดับก่อนหน้า
.
ล่าสุดทีมสหวิทยาการซึ่งประกอบด้วยนักวิทยาศาสตร์นานาชาติจากหลายสาขาวิชา นำโดยนักคณิตศาสตร์จากมหาวิทยาลัยอ็อกซ์ฟอร์ดของสหราชอาณาจักร ยังค้นพบเพิ่มเติมถึงความมหัศจรรย์ของตัวเลขในทางชีววิทยา โดยได้ทราบว่าความหลากหลายทางพันธุกรรมของสิ่งมีชีวิต สามารถจะเกิดขึ้นได้เองตามธรรมชาติด้วยทฤษฎีจำนวน (number theory) ที่แฝงอยู่ในโครงสร้างของสารพันธุกรรมอย่างดีเอ็นเอและอาร์เอ็นเอนั่นเอง
.
ผลการศึกษาดังกล่าว ได้รับการตีพิมพ์เผยแพร่ในวารสารของราชสมาคมแห่งกรุงลอนดอน (Journal of The Royal Society Interface) โดยดร.อาร์ด ลูอิส ผู้นำทีมวิจัยระบุว่า
.
“ความงดงามของทฤษฎีจำนวน ซึ่งเป็นส่วนหนึ่งของวิชาคณิตศาสตร์บริสุทธิ์ ไม่ได้อยู่ที่ความสัมพันธ์เชิงนามธรรมระหว่างบรรดาจำนวนเต็มที่มาบวกลบคูณหารกันด้วยฟังก์ชันเลขคณิต (arithmetic function) เท่านั้น แต่ยังอยู่ที่โครงสร้างทางคณิตศาสตร์ที่แฝงฝังอยู่ในระดับลึกของโลกแห่งธรรมชาติอีกด้วย”
.
ด้วยเหตุนี้ ทีมวิจัยของดร.ลูอิส จึงมุ่งให้ความสนใจกับหลักการทางคณิตศาสตร์ ที่อยู่เบื้องหลังกลไกวิวัฒนาการของสิ่งมีชีวิตต่าง ๆ ซึ่งกระบวนการนี้เริ่มต้นที่โครงสร้างระดับโมเลกุลของสารพันธุกรรม
.

ภาพจำลองตำแหน่งที่เกิดการกลายพันธุ์ในดีเอ็นเอ
การกลายพันธุ์ (mutation) หรือการเปลี่ยนแปลงลำดับเบสที่มีโอกาสเกิดขึ้นได้เป็นครั้งคราว เมื่อเซลล์มีการลอกแบบเพื่อผลิตซ้ำดีเอ็นเอและอาร์เอ็นเอ สามารถนำไปสู่ความหลากหลายทางพันธุกรรม และเป็นจุดเริ่มต้นวิวัฒนาการของสิ่งมีชีวิตชนิดพันธุ์ใหม่ ๆ ที่แตกแขนงแบ่งแยกเชื้อสายออกมาจากต้นตระกูลได้
.
ทีมผู้วิจัยจึงต้องการจะทราบว่า มีหลักการทางคณิตศาสตร์ใดที่คอยกำกับควบคุมโอกาสเกิดการกลายพันธุ์อยู่หรือไม่ รวมทั้งต้องการจะทราบว่า หลักคณิตศาสตร์ดังกล่าวสามารถส่งเสริมให้เกิดความเฟื่องฟูในการกลายพันธุ์ (mutational robustness) หรือโอกาสที่จะเกิดความเปลี่ยนแปลงทางพันธุกรรมในระดับสูงได้หรือไม่ด้วย
.
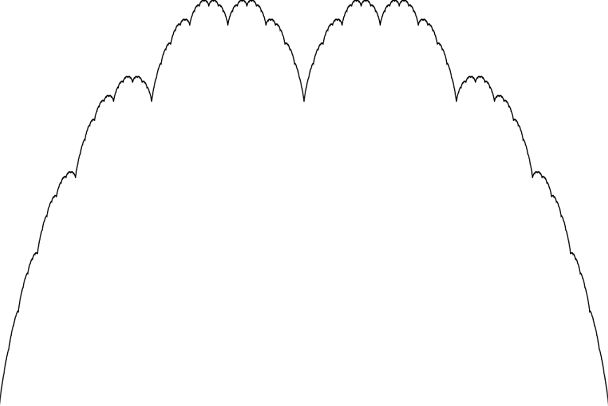
ตัวอย่างของเส้นโค้งบลองมองช์ (Blancmange curve)
ดร.ลูอิสและคณะได้ใช้แบบจำลองคอมพิวเตอร์ ทำการวิเคราะห์โครงสร้างการพับตัวของโปรตีนในเซลล์ รวมทั้งโครงสร้างขนาดเล็กจิ๋วของอาร์เอ็นเอ เพื่อค้นหาแบบแผนทางคณิตศาสตร์ที่อยู่เบื้องหลังลำดับพันธุกรรม ซึ่งเป็นพิมพ์เขียวกำหนดการเกิดลักษณะต่าง ๆ ในสิ่งมีชีวิต
.
ผลปรากฏว่าตัวอย่างโปรตีนในเซลล์ที่นำมาศึกษานั้น สามารถจะเกิดความผิดพลาดในการลอกแบบและผลิตซ้ำสารพันธุกรรมได้สูงถึง 66% โดยไม่ทำให้การถ่ายทอดพันธุกรรมดั้งเดิมของตัวมันเองได้รับผลกระทบ
.
ปรากฏการณ์เช่นนี้เรียกว่า neutral mutation หรือการกลายพันธุ์ที่ไม่แสดงออก สามารถพบได้ทั่วไปในมนุษย์และสิ่งมีชีวิตอื่น ๆ โดยลำดับพันธุกรรมที่มีการกลายพันธุ์จะไม่แสดงผลให้เห็นเป็นลักษณะทางกายภาพหรือพฤติกรรมใหม่ ๆ ที่ผ่าเหล่าออกมาในทันที แต่จะสะสมตัวและถ่ายทอดไปสู่รุ่นถัดไป ซึ่งมักจะเกิดการกลายพันธุ์เพิ่มเติมและจะนำไปสู่วิวัฒนาการของสิ่งมีชีวิตชนิดพันธุ์ใหม่ได้ในระยะยาว
.

ขนมพุดดิ้งบลองมองช์ มีรูปทรงที่เป็นเอกลักษณ์เฉพาะ
ทีมผู้วิจัยพบว่ากระบวนการข้างต้นมีความสำคัญและจำเป็นอย่างยิ่ง ในการเปิดโอกาสให้ธรรมชาติเต็มไปด้วยความหลากหลายทางชีวภาพ ทั้งยังเป็นกลไกที่ผลักดันให้เกิดวิวัฒนาการของสิ่งมีชีวิตได้ดีที่สุด โดยแบบแผนทางคณิตศาสตร์ที่กำหนดสัดส่วนซึ่งนำไปสู่ความเฟื่องฟูในการกลายพันธุ์ เป็นไปตามหลักการพื้นฐานของทฤษฎีจำนวนที่เรียกว่า “เศษส่วนผลรวมของเลขแต่ละหลัก” (digit sum fraction)
.
แบบแผนดังกล่าวสามารถแปลงเป็นรูปทรงเรขาคณิตได้ โดยโอกาสเกิดการกลายพันธุ์จะเป็นไปตามแนวโน้มของ “เส้นโค้งบลองมองช์” (Blancmange curve) ซึ่งเป็นชื่อของขนมพุดดิ้งสีขาวที่มีรูปทรงเป็นเอกลักษณ์เฉพาะ
.
เส้นโค้งบลองมองช์จัดเป็นวัตถุทางเรขาคณิตชนิดหนึ่งที่มีคุณสมบัติในการทำซ้ำตนเอง ถือเป็นโครงสร้างทางเรขาคณิตที่เกิดจากการแตกออกหรือแยกออกจากโครงสร้างทางเรขาคณิตเดิม โดยส่วนที่แตกออกมาจะยังคงรูปทรงเรขาคณิตของเก่าเอาไว้ แต่จะมีการลดขนาดลงเรื่อย ๆ
.
ดร.ไวภพ โมหันตี สมาชิกทีมวิจัยจากคณะแพทยศาสตร์ มหาวิทยาลัยฮาร์วาร์ดของสหรัฐฯ กล่าวสรุปว่า “ดูเหมือนว่าหลักชีววิทยาของธรรมชาติจะรู้จักทฤษฎีจำนวน รวมทั้งสัดส่วนเรขาคณิตเป็นอย่างดี โดยธรรมชาติใช้แบบแผนของคณิตศาสตร์บริสุทธิ์ดังกล่าว เพื่อเปิดโอกาสให้มีความเฟื่องฟูในการกลายพันธุ์ระดับสูงสุด ซึ่งจะปูทางไปสู่วิวัฒนาการของสิ่งมีชีวิตที่รุ่มรวยและหลากหลาย”
ที่มา : BBC https://www.bbc.com/thai/articles/cndeew0er6ro



